(40 points)
A factory has a bin packing robot at the end of an assembly line. There are exactly two bins open, and the robot packs items into any one of the open bins, one by one sequentially. The bins are identical, and one bin can accommodate a set of items up to a given weight limit. More precisely, the robot can perform the following four instructions:
A pack instruction can only be executed if the weight of the current item plus the sum of the weights of the items already in the bin does not exceed the limit. You are given the sequence of weights of items and a weight limit that is constant for all the bins. Write a program that computes the minimal number of bins needed by the robot to pack all items into them.
The input file contains integer numbers. The first line of input file contains the weight limit L (1 <= L <= 100). This limit applies to all bins. The second line contains the number of items N (1 <= N <= 5000). Each of the following N lines contains the weight of an item. Each weight is at least 1 and at most L.
Write on the first line of output file the minimum number of bins needed to pack all items.
BINPACK.IN 8 6 4 2 5 3 5 4 BINPACK.OUT 3
(40 points)
You are given a rectangle whose side lengths are integer numbers. You want to cut the rectangle into the smallest number of squares, whose side lengths are also integer numbers. Cutting can be performed with a cutting machine that can cut only from side to side across, parallel with one side of the rectangle. Obtained rectangles are cut separately.
The input file contains two positive integers in the first line: the lengths of the sides of the rectangle. Each side of the rectangle is at least 1 and at most 100.
The output file consist of one line on which your program should write the number of squares resulting from an optimal cutting.
CUTS.IN 5 6 CUTS.OUT 5
(20 points)
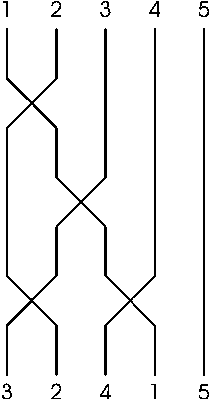
The electrician Fero has just finished the installation of the new cable in the building of the CEOI secretariat. The cable consists of N wires and connects the computer room and CEOI secretary office. In the computer room Fero labeled the wires with numbers from 1 to N from left to right. Because the cable was long, sometimes some of wires crossed between the computer room and the office (each pair of wires crosses at most once; at each moment only neighbouring wires may cross). So in the office the wires were not ordered the same way (see figure 1).
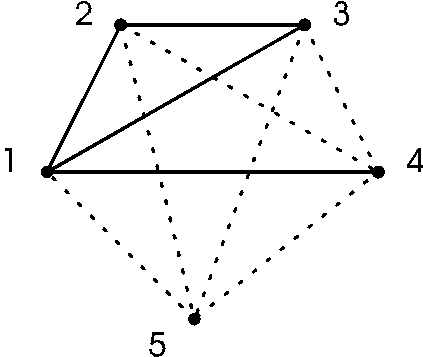
To know how these wires are crossed Fero drew the graph on the wall near the cable end in the computer room. The vertices represented wires and edges represented wire crosses. There is an edge between vertices a and b if and only if the wires a and b are crossed somewhere on the way (see figure 2 for graph representing situation in figure 1).
The cable does not function properly now. Unfortunately Fero broke his leg yesterday. We have another electrician but he is not so experienced in graph theory. He needs to know the order of wires at the end of the cable in the CEOI secretary office to correct this fault.


In the input file there are several blocks of data. The first line of each block contains two numbers N and M separated by a space, where N (1 <= N <= 100) is the number of wires in the cable and M is the number of wire crosses. This is followed by M lines each containing pair of integers A, B separated by a space (1 <= A,B <= N) representing the cross of cable wires A and B somewhere on the way. After the last block there is a line with two numbers 0.
For each block of the input file the output file contains a single line with the list of wire numbers in order as they appear at the second end of the cable (N numbers separated by space) or the message "IMPOSSIBLE" if no order is represented by given graph.
ELECTRIC.IN 5 4 1 2 1 3 2 3 1 4 0 0 ELECTRIC.OUT 3 2 4 1 5