Home I n t e r n e t   C o n t e s t i n t e r n e t

c o n t e s t		 C E O I

2 0 0 0


Regulations

Schedule

Organising
Team

Cluj&Romania

Sponsors

Secretariat

Internet Contest

Links


___________
Web design: Vivi

[ The rules | Read the problems | Submit solutions | Results | Downloads ]

Day one problems are available here.

Day 2
[ Problem 4 | Problem 5 | Problem 6 ]



Problem 6 : Enlightened landscape

Consider a landscape composed of connected line segments: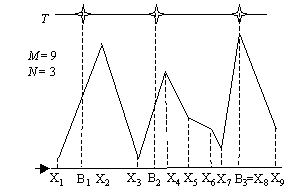

Above the landscape, N light bulbs are hang at the same height T in various horizontal positions. The purpose of these light bulbs is to light up the entire landscape. A landscape point is considered lit if it can "see" a light bulb directly, that is, if the line segment which links the point with a bulb does not contain any other landscape segments point.

Task
Write a program that determines the mi-ni-mum number of light bulbs that must be switched on in order to illuminate the entire landscape.

Input
Input file name: LIGHT.IN
Line 1: M
  • An integer, the number of landscape height specifications, including the first and the last point of the landscape.
    Lines 2..M+1: Xi Hi
  • Two integers, separated by a space: the landscape height Hi at horizontal position Xi, 1 <= i <= M; for 1 <= i <= M-1 we have Xi+1 > Xi; any two consecutive specified points identify a segment of line in the landscape.
    Line M+2: N T
  • Two integers, separated by a space, the num-ber of light bulbs and their height coordinate (altitude). The bulbs are numbered from 1 to N)
    Line M+3: B1 B2 ... BN
  • N integers, separated by spaces: the hori-zon-tal coordinates of the light bulbs Bi+1 > Bi, 1 £ i £ N-1;

    Output
    File name: LIGHT.OUT
    Line 1: K
  • An integer: the minimum number of light bulbs to be switched on.
    Line 2: L1 L2 ... LK
  • K integers, separated by spaces: the labels of the light bulbs to be switched on spe-cified in increasing order of their horizontal coordinates.

    Limits
  • 1 <= M <= 200
  • 1 <= N <= 200
  • 1 <= Xi <= 10000 for 1 <= i <= M
  • 1 < T <= 10000
  • 1 <= Hi <= 10000 for 1 <= i <= M
  • T > Hi for any 1 <= i <= M
  • X1 <= B1 and BN <= XM
  • The task always has a solution for the test data. If there are multiple solutions, only one is required.

    Example 
    LIGHT.IN          LIGHT.OUT 
6                 2
1 1               1 4
3 3
4 1
7 1
8 3
11 1
4 5
1 5 6 10
    •