Home I n t e r n e t   C o n t e s t i n t e r n e t

c o n t e s t		 C E O I

2 0 0 0


Regulations

Schedule

Organising
Team

Cluj&Romania

Sponsors

Secretariat

Internet Contest

Links


___________
Web design: Vivi

[ The rules | Read the problems | Submit solutions | Results | Downloads ]


[ Problem 1 | Problem 2 | Problem 3 ]

Problem 2 : The Caterpillar

Definition: A caterpillar is a particular kind of tree with the following property: there is a central chain such that each of the tree's nodes lie either on the central chain, or they are adjacent to that chain. Below there are shown two caterpillars. The darkened nodes indicate the chain.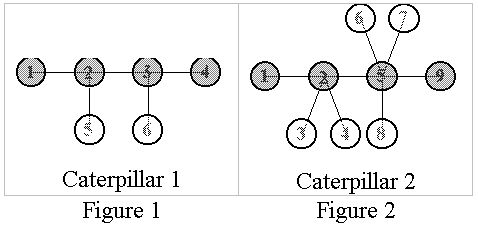

The chain is not necessarily unique. For example, another possible chain for the second caterpillar is 3-2-5-9.

Task
Given a caterpillar with N nodes, write a program which labels the nodes with numbers from 1 to N such that:
  • each label from 1 to N is used exactly once;
  • no two edges in the tree have the same absolute value of the difference between the labels of their adjacent nodes.

    For the second caterpillar above, a possible labeling is indicated below along with the corresponding differences on the edges: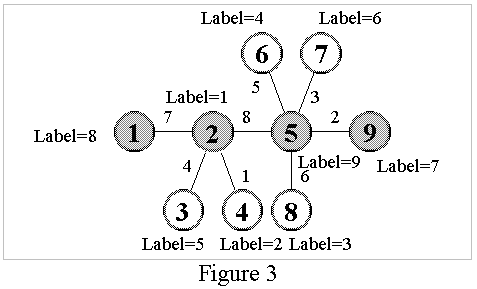



    Input
    File name: CP.IN
    Line 1: N
  • one integer, the number of nodes;
    Lines 2..N: X Y
  • two integers, separated by a blank, which are two adjacent nodes connected by an edge.

    The input data is correct, and the input tree is a caterpillar.

    Output
    File name: CP.OUT
    Line 1: L1 L2 ... LN
  • N integers, separated by blanks, where Li represents the label associated with the node i.

    If there are multiple solutions, only one is required. If no labeling is possible, the output file should contain only one line with the word: IMPOSSIBLE

    Limits
  • 2 <= N <= 10000

    Example
    The following input (CP.IN) describes the caterpillar from the Figure 2 and the output (CP.OUT) the labeling from the Figure 3. 
    CP.IN    CP.OUT (one possible solution)
9	    8 1 5 2 9 4 6 3 7
1 2
6 5
5 7
4 2
2 3
8 5
2 5
5 9
    •